המדע מבוסס במידה רבה על הסכמות – כשמצטבר מספיק מידע שמבסס אותה, תיאוריה הופכת לקונצנזוס ונחשבת אמת. אבל לפעמים הקונצנזוס הזה הופך מברכה לסכנה
הפרויקט המדעי בימינו משלב הרבה מאוד אנשים שעובדים יחד למען אותה מטרה: הרחבת גבולות הידע האנושי. ניתן לדמות את המדענים לפועלי בניין שמשתפים פעולה בבניית מגדל גבוה, וכל אחד מהם מוסיף בתורו עוד קרש ועוד לבנה למבנה. ככל שמצטבר הידע בתחום מסוים, המגדל שלם ויציב יותר, ואפשר יותר ויותר להסתמך עליו לחקר תחומים אחרים ולחשיפת תגליות חדשות. כשמצטברות מספיק ראיות לנכונותה, תיאוריה נחשבת לאמת מדעית, ויידרשו ראיות כבדות משקל כדי לערער אותה.
המדען הדגול אייזק ניוטון ניסח היטב את הרעיון הזה במכתב ששלח לעמיתו ויריבו רוברט הוק (Hooke): "אם הרחקתי ראות יותר מאחרים, אין זאת אלא מפני שעמדתי על כתפי ענקים". הקונצנזוס המדעי מבוסס על עבודותיהם של מדענים רבים, המשתלבות יחד ליצירת בסיס איתן שעליו אפשר לעמוד בבטחה כדי לחשוף תגליות נוספות.
אם כן, הקונצנזוס המדעי הוא כלי חיוני שמאפשר למדע להתקדם ולהתפתח בלי שהעוסקים בו יידרשו להמציא שוב ושוב את הגלגל מחדש. אולם לעיתים הוא עלול להפוך מברכה לאבן נגף המקשה על ההתקדמות המדעית התקינה: לפעמים לבנה אחת במגדל מאיימת להתפורר, אך מעליה כבר נבנו קומות רבות, ויש חשש שאם נוציא אותה המגדל כולו יתמוטט.
זה מה שקורה למשל כשמתברר שמחקרים קאנוניים, שרבים התבססו עליהם, הם שגויים או לא מלאים, ועל כן מרחף סימן שאלה גדול מעל כל גוף הידע שנבנה עליהם. במקרים אחרים, תגלית חדשה סותרת את הידע שנצבר בתחום במשך שנים רבות, ולכן היא מתקבלת בספקנות רבה ומדענים חשובים דוחים אותה מכול וכול. ויש גם מקרים שבהם מספיקה שגיאה אחת של מדען רב השפעה כדי להטות את הקונצנזוס המדעי למשך שנים רבות.
הסכמה נרחבת וגורפת הופכת תיאוריה לקונצנזוס, אך מה שנחשב לאמת היום יכול להפוך לטעות מחר. הסכמה בלחיצת ידיים | iQoncept, Shutterstock
השגיאה הטעונה של מיליקן
זה בדיוק מה שקרה בפרשת ניסוי טיפת השמן של הפיזיקאי רוברט אנדרוז מיליקן (Millikan), שמדד לראשונה את מטען האלקטרון, בשנת 1909. במהלך הניסוי השתמש מיליקן בשדה חשמלי כדי ללכוד טיפות שמן בעלות מטען חשמלי, ומצא את גודל השדה שיגרום להן לרחף באוויר. על ידי כך הוא הראה שהמטען החשמלי משתנה ביחידות בדידות קטנות, ולא באופן רציף, ושגודלה של כל יחידה קטנה כזאת הוא המטען החשמלי של אלקטרון בודד.
ניסוי טיפת השמן נחשב גם כיום לניסוי יצירתי, חכם ויפה במיוחד, ומיליקן זכה בזכותו בצדק רב בפרס נובל לפיזיקה בשנת 1923. אחרי המדידה הראשונה שעשה מיליקן, מדענים מצאו דרכים נוספות למדוד את מטען האלקטרון. אך הפלא ופלא – בעוד שמדידות שנעשו זמן קצר אחרי הניסוי של מיליקן הראו ערכים קרובים מאוד למדידה המקורית, אלה שנעשו עשרים שנה לאחר מכן כבר מדדו ערכים שונים לחלוטין. אומנם במונחים אבסולוטיים הפער בין המטען שמדד מיליקן למטען הידוע כיום הוא קטן, ועומד על כ-0.6 אחוז בלבד, אבל מאחר שטווח השגיאה של המדידה הרבה יותר קטן, מדובר בגודל שונה מהותית שלא היה אמור להימצא במדידות תקינות ואובייקטיביות.
איך יכול להיות שמדידות שונות של אותו גודל פיזיקלי יניבו ערכים שונים מאוד? לימים התברר שהייתה למיליקן טעות חישוב בניסוי שלו, ובעקבות זאת המטען שייחס לאלקטרון לא היה מדויק. אך מאחר שהניסוי שלו היה יפה ומשכנע, הערך שמצא התקבל מייד כאמת. פיזיקאים שביצעו את הניסויים הבאים חששו לפרסם תוצאות שיסתרו את ממצאיו, שנחשבו אמינים ומדויקים. כך קרה שבמקום שהטעות תתוקן, במשך שנים המדידות שנעשו למטען האלקטרון עלו בצעדים זעירים, בלי להתרחק יותר מדי מהמדידה המקורית השגויה. נדרשו עוד עשרות שנים עד שהמדידות התייצבו על הערך המקובל כיום.
מיליקן שגה כמובן בתום לב, ולא עשה דבר כדי להטות מחקרים עתידיים כך שיגבו את ממצאיו. אך הקונצנזוס המדעי שהתהווה סביב שיטת הניסוי שלו וממצאיו סיכל באופן סביל ובלתי מכוון כל ערעור על הערך שקבע למטען האלקטרון.

ניסוי חכם ופורץ דרך, שהתברר כי נתן ערכים שגויים עקב טעות חישוב. מדגים את הצד הרע של קונצנזוס. ניסוי טיפת השמן של מיליקן, 1909 | מקור: ויקיפדיה, נחלת הכלל
מחסום קשה למעבר
במקרה של מטען האלקטרון, מדענים סבלו בעיקר מזהירות יתר, שהניאה אותם מלפרסם ממצאים שסתרו את הקונצנזוס המדעי. מצב לא פחות מזיק הוא מה שעלול לקרות למדענים שמגלים תופעה חדשה ולא מוכרת, אך מוצאים את עצמם מתמודדים עם התנגדות ערה, ואפילו איבה אישית מצד מדענים אחרים שמתבצרים מאחורי הקונצנזוס. במקרים כאלה, קהילת אנשי המדע העוסקים בתחום המחקר הרלוונטי, או לפחות מדענים מובילים בה, שמים את כל כובד משקלם, מתוך שמרנות או קנאות לרעיונותיהם, כדי לדחות את הרעיונות החדשים הסותרים את מה ש"כולם יודעים".
מפורסם במיוחד סיפורו של הכימאי הישראלי דן שכטמן, שאומנם זכה בפרס נובל לכימיה בשנת 2011 על גילוי הקוואזי-גבישים, אך רק אחרי שנים רבות של מאבק מול עמיתיו לתחום. במשך שנים רבות היה ידוע שחומרים מוצקים יכולים להופיע בתצורה של גבישים, והיה ברור לכול שגבישים הם תמיד חומרים שהסידור שלהם במרחב הוא מחזורי ואחיד, כמו המשבצות בלוח דמקה, אך באופן תלת-ממדי. מבנה הגביש נשאר זהה בכל אזור שמסתכלים בו. אבל באפריל 1982, במהלך ניסוי שביצע במעבדתו, גילה שכטמן משהו מוזר: החומר התגבש בסדר שאינו מחזורי מלא, כך שבכל מקום שהסתכל בו נראתה תבנית מסודרת אחרת. הוא קרא להם "קוואזי-גבישים" (מעין-גבישים).
שכטמן הבין שהוא גילה תופעה חדשה למדע, אך ניסיונותיו לפרסם את ממצאיו בכתבי עת מדעיים נתקלו בהתנגדות עזה, עד כדי עוינות. בראש מתנגדיו התייצב הכימאי המפורסם לינוס פאולינג (Pauling), חתן פרסי נובל לכימיה ולשלום. בשיא העימות הוא אף אמר, "אין קוואזי-גבישים, יש רק קוואזי-מדענים". כמו כן הוא קרא לשכטמן ללכת "לקרוא ספר על גבישים", וגם דחף את המנחה האקדמי של שכטמן לסלק אותו מקבוצת המחקר שלו. חלפו כמה וכמה שנים עד שמספיק מדענים הסתקרנו די הצורך מטענותיו של שכטמן כדי לנסות לצפות בעצמם בקוואזי-גבישים. ככל שהצטברו הממצאים החדשים התגבש קונצנזוס חדש, שהפעם כלל בתוכו את הקוואזי-גבישים של שכטמן.

במשך שנים רבות מושא ללעג ולהתנשאות מצד קהילת המדע. דן שכטמן (שמאל) במכון הלאומי לתקנים וטכנולוגיה בארצות הברית, 1985 | מקור: H. Mark Helfer, Science Photo Library
ההיסטוריה של המדע שופעת דוגמאות רבות לאנשי מדע פורצי דרך שנאלצו להיאבק מול הקונצנזוס המדעי של תקופתם, לעיתים ללא הצלחה. למשל הרופא ההונגרי איגנץ זמלווייס (Semmelweis), שנחשב היום לאחד מאבות האפידמיולוגיה, הפך ללעג ולשנינה בבית החולים שבו עבד, במאה ה-19 לפני גילוי החיידקים, כשעמיתיו הרופאים זלזלו בטענתו שחיטוי הידיים מונע מחלות. ואילו תיאוריית נדידת היבשות שהגה המדען הגרמני אלפרד לותר וגנר (Wegener) שהתקבלה על ידי הקהילה הגיאולוגית רק כעשרים שנה אחרי מותו.
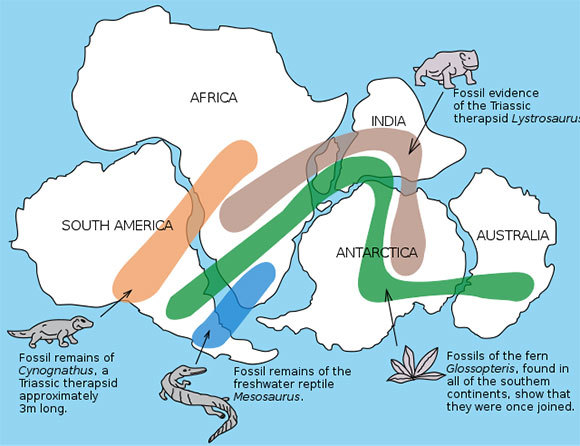
תיאוריית נדידת היבשות שהגה אלפרד לותר וגנר התקבלה על ידי הקהילה המדעית רק לאחר מותו. יבשת גונדוואנה לפני כ-550 מיליון שנה | מקור: Osvaldocangaspadilla, Wikiwand
להגן על הקונצנזוס המדעי מפני עצמו
לקונצנזוס המדעי יש חשיבות מכרעת ליכולתנו לקדם את הידע האנושי. אלמלא הוא, לא היה לנו בסיס משותף לפעול מתוכו וכל אחד היה צריך לבנות את מגדל הידע של תחומו בכוחות עצמו. יתרה מכך, הקונצנזוס המדעי מאפשר לקהילה המדעית לתת לציבור תשובות מוסמכות ומבוססות-ראיות במחלוקות ציבוריות הנוגעות בסוגיות מדעיות – למשל בדיונים על חיסונים או על הדרישה להפנות משאבים לבלימת שינויי האקלים.
ובכל זאת, הישענות מופרזת עליו עלולה להוביל את המדע לכיוונים שגויים או לעכב את התקדמותו. אין לדעת אילו רעיונות נכונים וחדשניים הקהילה המדעית דחתה מתוך שמרנות גרידא, ואילו פריצות דרך סוכלו משום שאיש לא העז להגות אותן מלכתחילה. רק העתיד יגלה אם אנו דוגלים כיום ברעיונות שגויים שנשארים בקאנון המדעי בעקבות הישענות על קונצנזוס מוטעה. אף על פי שרובם הכמעט מוחלט של הרעיונות שסותרים את הקונצנזוס המדעי הם אכן שגויים, יש לראות בתהיות הללו אותות אזהרה מפני הסתמכות עיוורת על "מה שכולם יודעים".

ההתנגדות העזה שקריאתו להיגיינה וחיטוי עוררה אצל רופאים בני תקופתו הובילה להתמוטטות עצבים ואשפוז במוסד לחולי נפש. איגנץ זמלווייס | מקור: Jeno Doby, Wikiwand
השיטה המדעית מספקת לעוסקים בה אוסף כלים שמטרתם בין השאר למנוע טעויות כאלה. אחד הכלים החשובים ביותר נגד קבלה לא ביקורתית של ממצאים, כפי שקרה בפרשת המטען החשמלי של האלקטרון, הוא הרפליקציה: שחזור בלתי תלוי של מחקרים שנעשה בידי חוקרים אחרים במקום אחר. הציפייה היא שמחקרים טובים יניבו ממצאים דומים כשמשחזרים אותם. שדה הפסיכולוגיה החברתית, לדוגמה, חווה בימים אלה משבר, אחרי שהתברר שמחקרים רבים בתחום – לרבות תיאוריות ותיקות שהיה סביבן קונצנזוס – אינם ניתנים לשחזור, חלקי או מלא. בעקבות זאת מתנהל כעת מאמץ מאורגן לבחון מחדש את שיטות המחקר ששימשו במחקרים שנעשו בתחום ולשחזר אותם.
אמצעי נוסף שיכול לסייע הוא הנוהג לחשוף את כל הנתונים שעליהם התבסס מחקר שהופיע בכתב עת מדעי. כך אפשר להבטיח בסבירות גבוהה יותר שהדיון על אמינות המחקר ועל נכונות ממצאיו יתבסס על נתונים ולא על דעותיהם האישיות של מדענים. ומעל לכל, מכל מדען ומדענית נדרשת מידה בריאה של ספקנות ושל צניעות. הקפדה עליהן תבטיח שלא יתבצרו בעמדותיהם, או בעמדת הקונצנזוס, אם הנתונים הנצפים מעידים שהאמת המדעית היא שונה ממה שסברו.
