Cooperation, Betrayal and Conflict -
Exploring the Prisoner’s Dilemma

In many situations in life we are required to cooperate with others, oftentimes prioritizing the collective good over our own immediate interests. Examples include actions such as reducing the use of polluting fuels to mitigate climate change, yielding to others at an intersection, getting vaccinated against COVID-19 to protect at-risk groups, even if we are likely to easily overcome the disease ourselves, voluntarily validate tickets when riding a bus, since if everyone rides for free, public transportation will be unsustainable, and countless other decisions, both significant and trivial.

The situations mentioned above are examples of the prisoner’s dilemma, a concept in the field of mathematics known as Game Theory, which studies decision making and strategic interactions among two or more players. A game involves two or more active parties, called “players”, who must choose courses of action based on well-defined rules that ultimately determine the outcome of the game in a clear and quantifiable way. Game theory assumes the players seek to achieve the best possible outcome for themselves, based on rational considerations, in accordance with the confines of the game’s conditions and rules.

The prisoner’s dilemma describes a game in which the two actors must each independently choose between two actions: “cooperation” or “betrayal”. Since each actor has two available choices, there are a total of four possible situations: both players cooperate, both players betray, or one player cooperates while the other betrays, and vice versa.

In game theory, players choose courses of action from strategies with well-defined rules. An image depicting individuals developing a strategy for playing chess | Shutterstock, AlisaRut

The Basic Dilemma

The term “Prisoner’s Dilemma” originates from a classical way of presenting the problem. The story goes as follows: two suspects are arrested by the police for a crime that took place, but there is only enough evidence to convict them of a smaller offense. To secure a conviction for the more serious crime the police need the suspects to confess. Each suspect is interrogated separately and has the choice to betray their partner by confessing or to cooperate with him and remain silent. If both suspects cooperate with each other and remain silent during their interrogation, they receive a relatively mild sentence, such as a one year in prison, because the police can only convict them of committing the lesser crime. If one suspect confesses on the other and the other remains silent, the confessor is granted a state witness status and goes free, while their partner receives a 20-year sentence for the more serious crime. If both confess, and thus both betray each other, they receive a reduced sentence of five years each, for admitting to the crime and assisting the investigation. This is, of course, a purely hypothetical situation used to demonstrate the concept, and should not be taken as an accurate portrayal of police interrogation practices or of the proper way to interrogate suspects, 

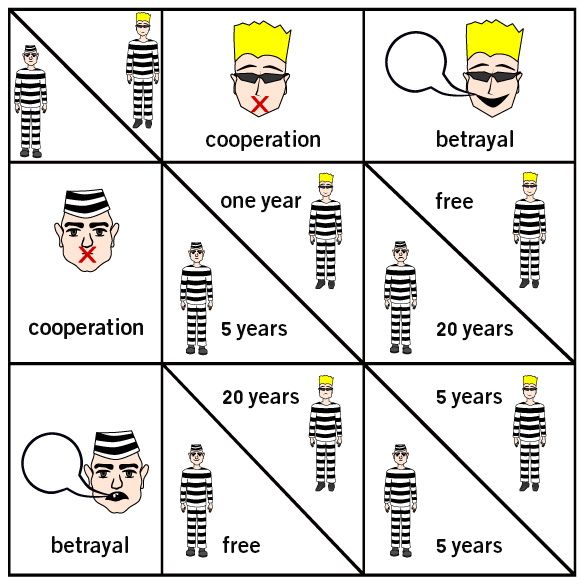
Each prisoner has the choice to betray their partner by confessing or to cooperate with him by remaining silent. The outcome is dependent on both their own decision and on their partner’s decision. A diagram that illustrates the different options and outcomes in the Prisoner’s Dilemma | Shutterstock, Sergey Merkulov

The prisoners’ problem is that each of them is interrogated separately by the police at the same time, which means that neither prisoner has any way of knowing what decision their partner will make. In this situation it’s better for each prisoner to betray his partner, regardless of the decision made by the partner. Why? Let’s examine the different options: if their partner chooses to remain silent, the prisoner should confess and go free instead of spending a year in jail because they also preferred to remain silent; if their partner confesses, our prisoner should certainly confess to the crime and sit in jail for only five years instead of twenty. The second prisoner uses the same reasoning, and both prisoners end up blaming each other, resulting in both going to jail for five years. 

In game theory, this type of situation is referred to as a Nash equilibrium: a situation in which each player knows that if they alone act differently, they will only lose. However, in this particular case, the equilibrium obtained is not the optimal outcome for either player. If both prisoners  trusted each other and remained silent during the interrogation, they would each only receive a sentence of one year in jail instead of five years!

Is this a contradiction? A paradox? A miscalculation? Not at all. The explanation is simple: there is a difference between an “optimal state” and a “steady state”. Personal cost-benefit considerations lead us to a steady state in which we do not depend on others and do not need to trust them. Thus, every criminal who informs and thus betrays their partner ensures that their personal fate will be better regardless of what their partner decides to do, and it does not benefit any criminal to change their behavior. However, in some situations, such as the prisoner’s dilemma, the steady state is not the optimal state, since the optimal state requires each player to trust their partner and entrust their fate to them. 

This is, in a nutshell, the trap of the Prisoner’s Dilemma. It’s a situation where if each player acts in their own best interest, a “Nash equilibrium” is achieved in which the outcome is not optimal for either player.

In the Prisoner’s Dilemma the equilibrium reached is not the optimal outcome for either criminal involved. Image of two women handcuffed together | Shutterstock, Zoka74 

An Iterated Prisoner's Dillemma 

That was the basic situation, which involved a one-off game. However, what if the same players had to repeat the game multiple times, as is often the case in real decision-making situations? It turns out that this change in the game’s circumstances also changes its course. Since there is an expectation of future rounds, each player can now punish his counterpart for betrayal by betraying them in the next round—a choice that didn’t exist in the single game mode. In this situation the dynamics of the dilemma become much more interesting. The two players can attempt to build mutual trust with one another, cooperate and improve their situation rather than repeatedly betraying each other in every round. This game is known as the “Iterated Prisoner’s Dilemma”.

What is the optimal strategy in an Iterated Prisoner’s Dilemma? In an experiment conducted by political scientist Robert Axelrod, experts were asked to design computer programs that would play 200 rounds of the Prisoner’s Dilemma against each other, such that each program would play according to the strategy deemed optimal by its programmer under the given circumstances. Various proposals were submitted by experts from different fields, ranging from simple strategies such as fixed cooperation or random decisions, to very complex ones. Surprisingly, the winner was one of the simplest and most intuitive versions, called “Tit for Tat” or “an eye for an eye”. The program begins with cooperation and then mirrors the opponent’s previous move. If the opponent cooperates, the program cooperates in the next round. If the opponent betrays, the program also betrays in the next round, and so on until the end.

This strategy has proven to be successful. The program was able to cooperate with cooperative opponents, and punished disloyal opponents. However, although it was the clear winner of the competition, we cannot determine whether this really is the optimal strategy. In fact, there’s no real optimal strategy in the ongoing game of the Prisoner’s Dilemma, because much depends on the sequence of actions chosen by the other players, as can be demonstrated through interactive versions of the game, in which players can see the impact of different strategies in different scenarios.

In the chicken game, two drivers drive towards each other on the same road | Illustration: Shutterstock, vetorlab2D

Games Similar to The Prisoner’s Dilemma: The Chicken Game and Real-Life Scenarios

Game theory offers several games similar to the Prisoner’s Dilemma, but fundamentally different. Here we’ll mention two games that are also considered important because many real-life situations resemble them.

The first game is known as “The Chicken Game”. The key difference between this game and the Prisoner’s Dilemma is that the worst outcome for both players is when both of them betray. In the classic example, two drivers head towards each other on the same road. The worst outcome for both of them is when neither of them moves aside, resulting in a head-on collision; the best outcome for each player is when their opponent moves aside and is deemed a coward (chicken), while the one who continues to drive in the center of the road is the winner, having proven his courage.

Reality offers many situations that resemble the chicken game. One of the most common and familiar scenarios for all of us is the one in which two parties in a coalition “flex their muscles” in a political argument and each one threatens to dissolve the coalition if its demands are not met. Both parties prefer to avoid dissolution, but each one hopes that the other will capitulate at the last minute, so it will be able to show its supporters that it stuck to its principles. Another example is when two countries that don’t want war engage in a standoff and threaten each other.  Despite both sides preferring to avoid war, which is clearly the worst possible outcome, each side wants the other to make concessions and neither wants to appear weak. As a result, both sides toughen their stance in the hope that the opponent will break, potentially leading to a war that neither side is truly interested in. 

In the stag hunt game there are two equilibrium points: one is when everyone cooperates, similar to the prisoner’s dilemma, and the other is when everyone betrays. An illustration of three hunters in the field | Shutterstock, kkhrustov

The second game, known as the “Stag Hunt”, in which a very large number of players can take part, differs from the prisoner’s dilemma in that it has two points of equilibrium: one is when everyone cooperates, similar to the prisoner’s dilemma, and another where everyone betrays. The game is named after a scenario that depicts a hunting expedition where the hunters have the choice to hunt a stag, which will provide enough meat food for everyone, but this outcome requires everyone’s cooperation. At any given moment each hunter can betray their friends and hunt a rabbit on their own. This would yield less meat than the amount he would get if he hunted a stag, but the rabbit is a certain catch,without depending on others. However, if one hunter chooses to hunt a rabbit, the stag will be scared off by the gunfire. 

Thus, it seems that for a single hunter it pays off to hunt a rabbit, because if one of his friends decides not to cooperate in the hunt, he will be left hungry, while cooperation is a gamble. On the other hand, it’s a gamble that may pay off. Betrayal naturally means making do with less but playing it safe. If all hunters cooperate, and completely trust each other, none of them has a reason to do anything else, and they can hunt the stag. This represents an equilibrium point. But the moment one of the hunters decides to hunt a rabbit, the only reasonable decision left for all the others is to follow suit and also hunt rabbits. This marks the second equilibrium point.

Many life situations are reminiscent of interactions between animals that can be compared to the prisoner’s dilemma. Two bears standing opposite each other | Shutterstock, EVILKA

The Prisoner’s Dilemma in the Animal World

The prisoner’s dilemma and similar scenarios are highly significant in the animal world. Many situations that concern interactions and mutual relationships between animals can be compared to the prisoner’s dilemma. The conclusions drawn from the previous discussion about relevant strategies for the prisoner’s dilemma are also important. Evolution has led many animals to adopt sophisticated game strategies in real-life “prisoners’ dilemma” scenarios. In many cases the players repeatedly play against each other, providing an opportunity to establish trust relationships - as we saw in the iterated prisoner’s dilemma.

In such contexts, the concept of an “evolutionary stable strategy” holds particular importance. In the computer program competition,  each player competes against the others in each round, but before the next round the composition of the population changes. The players with the lowest score become extinct, and those with higher scores reproduce at their expense, passing on their genes - or the game strategy they follow - to the next generation. This process closely resembles relationships and power games in the animal world, where organisms and animals “play” against each other. The winners are those who manage to produce offspring and pass on their tendency to adopt a particular strategy to the next generation. 

The  real world is of course much more complex: not all individuals always participate in the same game, the rules of the game may change suddenly, and many factors can affect the outcome, including randomness. However, at its core, the Prisoner’s Dilemma manages to capture the essence of cooperation between animals. This may explain why the behavior of many animals seems to follow strategies similar to the “eye for an eye” approach: they’re aggressive if attacked but cooperate with friendly members of their group.