These days, we keep hearing about rocket fire from Gaza along with successful interceptions by the Iron Dome system.
Here I will explain how rockets fly and what trajectory they take based on physical principles. I should clarify that I’m not familiar specifically with the Iron Dome system, nor do I have specific knowledge about intercepting rockets.
Let’s assume our interception system has an excellent radar. The radar emits electromagnetic radiation all over, and when that radiation hits objects in its way, such as a rocket, the radiation returned from them reveals precisely where the object is and how fast it’s moving.
The system has two tasks: Firstly, it needs to identify quickly where the rocket is about to hit, and secondly, where along its trajectory a missile should be fired to intercept it.
So, first, let’s figure out what movement the rocket is about to make. For simplicity, let’s start with the most basic, simplistic description of rocket movement, and then consider the real conditions in which they are fired. Then we’ll understand why the trajectory is more complicated and harder to judge and analyze.
Rockets and Trajectories
A rocket is generally a cylindrical motorized object, launched from a launcher. Unlike missiles, rockets have no guiding system, which means it does not correct its course during flight but rather flies in a regular ballistic trajectory, which we will explain shortly. Its upper part generally contains explosives, which are designed to explode on impact and cause damage. This is called a “warhead”.
There are, of course, many different types of rockets. They differ in their size, the size and weight of the warhead, and by the way they propel their motion, and hence their ranges differ as well.
Let’s assume the rocket is a simple body, whose angle is determined upon launch, and whose engine pushes it at a constant force from the time it is switched on until it is switched off. Then the rocket continues in a free-fall, influenced by gravity. After we understand this motion, we can discuss prediction of the site of impact and try to understand why it is so complicated to actually detect the rocket’s trajectory and intercept it in reality.

Iranian-made Fajr 5 rocket
First Phase: Take-off and Acceleration
In the first phase, the rocket is launched from a launcher that is aimed at a certain angle from the ground and the rocket engine propels it upwards at that angle. Unlike a cannon shell, the rocket engine continues to operate for some time after launch to accelerate the rocket. At this stage, assuming the simplest model, we’ll ignore drag and focus only on the forces applied by the engine and by the earth’s gravity.
The acceleration phase. The rocket engine propels it upwards at the angle it was fired. Right: Forces acting on rocket.
Second Phase: Freefall
After the engine runs out of fuel, and the rocket no longer emits fire and gases, only gravity and drag act on the rocket. We’ll ignore drag for now. Once the engine turns off, the rocket moves at the angle and speed it acquired up until the end of the acceleration phase. To understand this motion, we’ll break it into two axes: We’ll call the vertical axis Z and the horizontal axis X.
Along the horizontal axis, movement is very simple. No force acts on the rocket on this axis, so it will keep moving at a constant speed (V) until it hits the ground. The distance it will move along the X-axis equals V times t, the time of flight. t is determined by the movement along the vertical axis.
Along the vertical axis, movement is quite simple as well. The major force at work is gravity, and it makes the rocket accelerate to the ground at the acceleration g, which is approximately 9.8 meters per second squared. Since it was moving upwards until the engine switched off, it will continue moving up, but will slow down until it reaches its maximal height and start falling until it hits the ground. The trajectory of a rocket at this stage is shaped like a parabola.
Second phase: After the rocket engine runs out of fuel, it goes into free-fall, affected only by gravity.
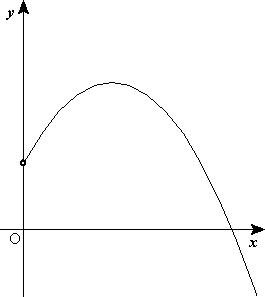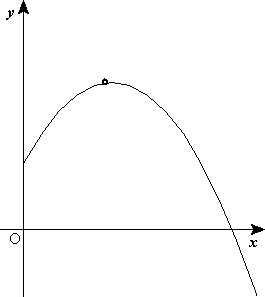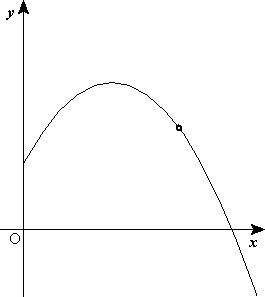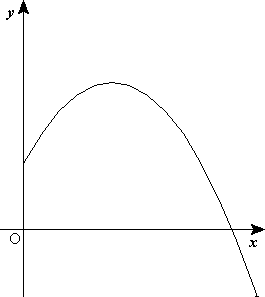
Trajectory of rocket in freefall, without drag.
Deviations from the Ideal Trajectory
So far we have described a simple trajectory. It seems that any radar that could identify the rocket in flight could also immediately calculate its trajectory until impact. However, in practice, many factors affect rocket flight.
One of the most significant factors is drag, or air resistance. Drag is a type of friction that depends on the speed of the rocket. The faster the rocket moves, the more drag acts on it, and always against the direction of movement.
Drag can be reduced by rocket design but not eliminated. It affects the simple movement we just described: it slows the rocket down, and makes it reach a lower altitude and fall closer to the launching point. Drag also depends on air density, which varies from altitude to altitude.
To feel the influence of drag on ballistic motion, you’re invited to use our applet. Launch objects from a cannon and see how they move depending on the angle of the launch, gravity and drag. Note that the shapes of different objects affect drag. The most aerodynamic shape in the applet is a shell, which has no engine, and begins free-fall upon launch.
Torque
So far we have treated the rocket as if it only moves in the Z and X axes. It also moves on the Y-axis, but in our analysis so far we included no force that could move it on this axis. The reason is that we treated the rocket as a body with no volume, essentially a point of mass. In practice, however, rockets have volumes and complex structures, and the forces acting on it may not act on it uniformly. One side may be affected more strongly than the other. This causes torque, which rotates the rocket and may drive it off course.
To understand why non-uniformly distributed forces might drive the rocket off course, imagine the following: Suppose you are standing with your arms spread to the sides and two friends are pushing you backwards from the palms of your hands. If they push with equal force, you will fall flat on your back, but if one pushes more strongly than the other, you might rotate as well as fall backwards. One side of your body is supposedly trying to move faster than the other. The same thing happens to the rocket when the forces acting on it aren’t uniformly distributed.
These inaccuracies might stem from a non-ideal launching pad or an imperfect engine or drag, which affects one side of the rocket more than another. Rocket structure, manufacturing defects and weather conditions are other major factors to consider.
Rocket developers cope with these phenomena in various ways, including adding wings at the sides of the rocket. The air passing through these wings causes the rocket to spin about itself as it flies. Here we will leave an open question - why does this rotation make it harder for the rocket to fly off course? Think of conservation laws. If you know the answer, feel free to include it in the comment section and we will discuss it.
Even after adding the wings, rockets will never be totally precise and there will always be some uncertainty about their trajectory. Even sophisticated rockets like the Iranian Fajr suffer from precision problems. A Fajr 3 fired at a target 40 km away may hit the ground in a radius of up to one kilometer from that target. Its exact impact site will be severely affected by the conditions the rocket faces in flight.
Sensing rockets, calculating trajectories and interception
Based on this knowledge, we can begin to understand what a system for detecting and intercepting rockets should do.
Firstly, it needs to identify the trajectory. At this stage, the system needs to locate the rocket and rapidly compute its trajectory and speed. The rocket is likely detected soon after launching, but as long as the engine is running and the rocket is accelerating, it is hard to estimate where it will fall. This is easier to compute as soon as free-fall begins. If the radar can detect what type of rocket its characteristics is based on, the system may be able to predict when the engine will turn off. Without this prior knowledge, prediction is difficult.
As free-fall begins, a radar providing data about the rocket’s altitude and speed, the trajectory is easy to compute without taking drag into account. In practice, forces such as drag must be incorporated to more accurately predict the rocket’s trajectory.
At this point, sophisticated algorithms kick in, which must be one of the most important components of the Iron Dome system. One of the most familiar ways to improve accuracy is to estimate the effect of drag based on the deviations of the rocket from the ideal trajectory as its motion begins. In this way, momentum loss can be quantified, drag can be estimated and the trajectory can be estimated more accurately.
In the operational system, sophisticated algorithms must constantly recompute the rocket’s trajectory based on data coming in from the radar. They most likely identify the effects of drag and incorporate historical data of known rocket trajectories.
After the rocket trajectory is computed, we must know if the rocket will hit an open area or not. If not, it will need to be intercepted, and the best place to intercept it should be found.
Even the best radars don’t analyze rocket trajectories completely, so it’s impossible to plan the precise trajectories of interception missiles such that they will hit the incoming rocket directly. Hence, according to publications on the Iron Dome, the intercepting missiles are fired into the rocket’s estimated trajectory but constantly receive corrections from the radar and are also equipped with their own tracking devices, allowing for rocket identification and trajectory adjustments.
Even so, missiles don’t hit rockets directly, but rather go as close as possible and explode nearby. The blast wave and shrapnel should hit the enemy rocket’s warhead and make it explode while airborne.

Iron Dome. Photo: Stavchansky Yaakov, Shutterstock
Summary
We saw that rockets are bodies controlled by simple forces, such as gravity and drag, and so have ostensibly simple physics that should be easy to predict and compute. However, without prior knowledge, such as the aerodynamic structures of the rockets, it is difficult to infer the forces at work and so complex algorithms must continuously track the rocket and refine its predicted trajectory.


